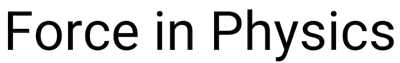In physics, tension refers to the pulling force transmitted through a wire, rope, or string when an object is connected to it. It is a force that stretches or elongates the material it acts upon. Tension is opposite to compression, which involves a pushing or squeezing force. For example, consider a block attached to a string passing over a pulley. When the block is suspended, the tension in the string arises from the force pulling it upward to counteract the force of gravity trying to pull it downward. The resulting balance between tension and gravity determines the block’s motion. If the tension in the string is greater than the force of gravity acting on the block, the block will accelerate upwards. If the tension is equal to the force of gravity, the block will remain in equilibrium, neither accelerating nor decelerating. However, if the tension is less than the force of gravity, the block will accelerate downwards.
Examples
Climbing rope

When a person climbs a mountain using a rope, the rope experiences tension. Tension is the force transmitted through the rope when it is pulled from opposite ends. In this scenario, the rope is taut and stretched as the climber’s weight pulls downward, and the anchor point or belayer’s hold pulls upward. The tension force in the rope enables the climber to ascend safely by providing the necessary support and preventing them from falling. The climber must trust the strength and integrity of the rope and its ability to withstand the tension force during the ascent.
Guitar

When a person plays a guitar, the strings of the instrument experience tension. As the individual presses down on the frets and plucks the strings, they get pulled from opposite ends and generate tension within the strings. This tension in the strings creates a force that is transmitted along their length. This force is known as the tension force. It is this tension force that allows the guitar strings to vibrate and produce sound when played, creating the melodic notes and tones that are characteristic of the instrument’s music. The amount of tension in the strings can be adjusted by tuning the guitar, which in turn influences the pitch and quality of the sound produced.
Twisted rope

When a rope is pulled by two hands in opposite directions, tension is created within the rope. This tension is a result of the forces applied by each hand, trying to stretch the rope. The tension force is the force that is transmitted along the length of the rope due to this pulling action. It is this tension force that keeps the rope taut and resists any attempts to stretch or elongate it further. The greater the force applied by each hand, the higher the tension in the rope.
Suspension bridge
In a suspension bridge, multiple cables are used to support the bridge deck and bear the load of traffic and other forces. When the weight of the bridge deck and the vehicles passing over it apply downward force on the cables, tension is generated within these cables. The tension force arises as the cables resist being stretched under the weight they support. This tension force runs through each cable and transmits the load from one end of the bridge to the other, which effectively holds the bridge in its suspended position. The cables’ ability to withstand this tension is crucial for the stability and structural integrity of the suspension bridge, making tension a vital component in ensuring safe and efficient bridge construction and operation.
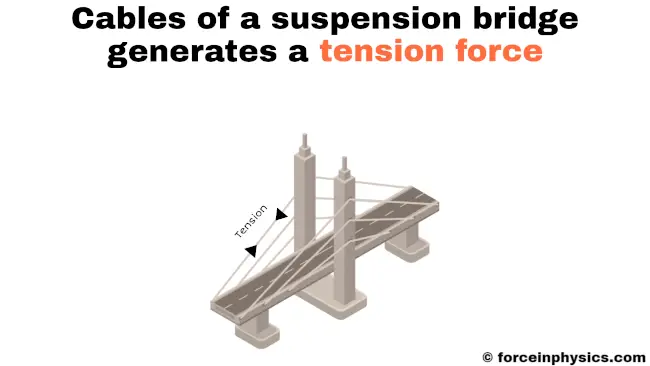
Towing
When a vehicle is being towed by a truck using a chain, the chain experiences tension as it gets pulled from opposite ends. This tension is a result of the forces applied to the chain as the truck moves forward and tows the vehicle behind it. The tension force running through the chain transmits the pulling force from the truck to the vehicle and allows it to be effectively towed. The chain’s ability to handle this tension is essential for ensuring a secure and stable towing process, as it prevents the chain from breaking or becoming loose during the towing operation.
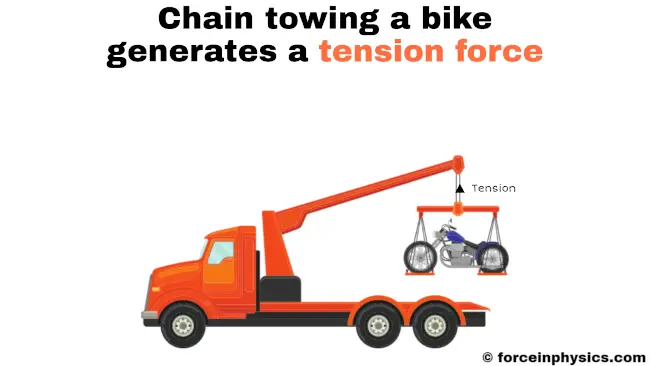
Barbed wire
When barbed wire is installed in a wire fence, it is tightly stretched and secured between posts. As a result, the wire experiences tension, which is the force that develops within the wire due to its elongation and resistance to being stretched. This tension is generated as the wire is pulled from opposite ends when it is being installed or tightened. The tension force runs through the length of the barbed wire, holds it firmly in place, and ensures that the fence remains sturdy and secure. This tension in the barbed wire is crucial for maintaining the integrity of the fence and providing a reliable barrier for various applications, such as agricultural fencing or perimeter security.
Hanging block
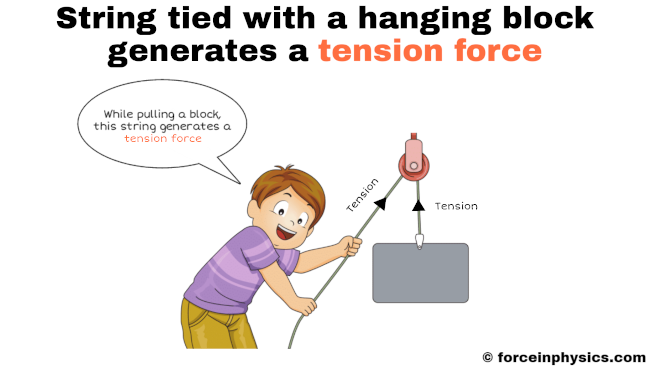
When a block is hung from a string, the string experiences tension, which is the force that develops within the string as a result of its elongation and resistance to being stretched. As the block hangs, the string is pulled from opposite ends where it is attached to the block and the support. This tension force runs through the length of the string supports the weight of the block and keeps it suspended. The tension in the string is essential for maintaining the equilibrium of the block and ensuring that it remains in place without falling. This example of tension in a string is common in various scenarios, such as when objects are suspended or when weights are lifted using pulleys or other mechanical systems.
Shoelaces

When shoes are hung or suspended, the shoelaces experience tension. This tension arises due to the weight of the shoes pulling down on the shoelaces from opposite ends. The force of gravity acts on the shoes, causing them to hang downward, which, in turn, generates tension in the shoelaces. The tension in the shoelaces helps support the weight of the shoes, ensuring that they remain securely hung.
Guy-wire
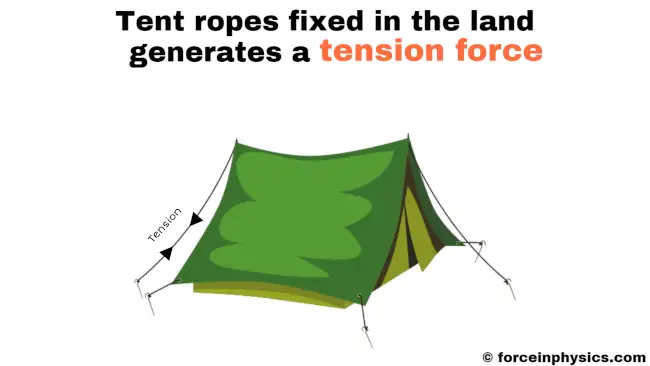
When setting up tents, guy-wires are used to provide stability and support. These guy-wires are fixed securely to the ground and are anchored to the tent structure. As they are tightened, they experience tension, which is a result of the force applied to the ropes from opposite ends. This tension is crucial for maintaining the integrity of the tent, as it counteracts external forces like wind or other factors that may cause the tent to collapse. The tension in the guy-wires distributes the load evenly and ensures that the tent remains stable and upright during various weather conditions. The tension force in the guy-wires is a vital component of tent construction and plays a significant role in the overall stability and functionality of the tent.
Wire rope

When a heavy hook is hung from a crane using a wire rope, the weight of the hook creates tension in the wire rope. As the hook is supported and secured by the wire rope, it exerts a downward force on the rope due to its mass. Simultaneously, the wire rope resists the force and pulls back upwards on the hook, creating tension in the rope. This tension force is essential for holding the heavy hook in place and preventing it from falling to the ground. The wire rope’s ability to withstand this tension is crucial for the safe and efficient operation of the crane, ensuring that heavy loads can be lifted and moved with precision and stability.
Tightrope walking
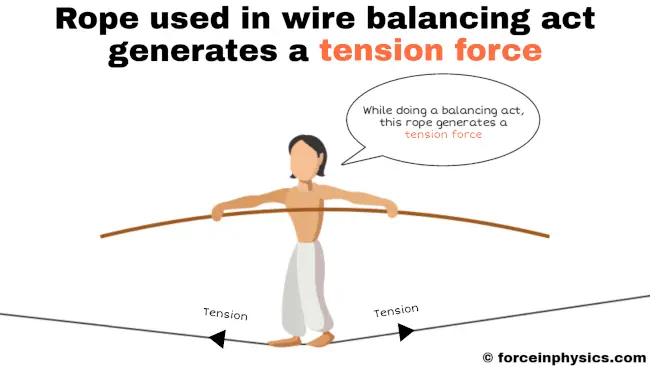
Tightrope walking is a captivating example that showcases tension in action. As the skilled performer balances and walks along the thin rope, the rope itself experiences tension. The tension arises from the opposing forces acting on the rope. On one hand, the performer’s weight pulls the rope downward, while on the other hand, the rope resists this downward force and pulls back upward on the performer. This tension force in the rope is crucial for maintaining the performer’s balance and preventing them from falling. It is the interplay between the performer’s weight and the rope’s resilience that allows for the mesmerizing display of tightrope walking. This feat showcases the significance of tension forces in achieving such remarkable balance and skill.
Fishing line

In fishing, a fishing line is used to catch fish. When a fish is caught on the line, the line experiences tension as it is pulled from opposite ends. This tension in the fishing line is a result of the force exerted by the fish as it tries to swim away. The tension force in the fishing line allows the angler to feel when a fish is biting and helps to reel in the catch.
Equation
The tension equation, FT = mg ± ma, allows for the calculation of the tension force experienced by an object attached to a string, rope, or cable. In this equation, FT represents the tension force, m is the mass of the object, g is the acceleration due to gravity, and a is the acceleration of the object. By using this equation, one can accurately determine the tension force acting on an object in various scenarios, such as when it is moving upward, moving downward, or at rest.
For instance, when an object is moving upward, the tension force is given by FT = mg + ma, considering the additional force needed to counteract gravity and accelerate the object upward. On the other hand, when the object is moving downward, the tension force is expressed as FT = mg – ma, taking into consideration the opposing forces of gravity and the acceleration of the object in the downward direction. When the object is at rest, the tension force equals the weight of the object, which gives FT = mg.
Practice problems
Problem #1
The tension force acting on a wooden plank with a mass of 5 kg, hanging from a rope and remaining stationary with no acceleration, needs to be calculated.
Solution
Given data:
- Mass of a wooden plank, m = 5 kg
- Tension force acting on a wooden plank, FT = ?
Using the equation, when an object is at rest:
- FT = mg
- FT = 5 × 9.81
- FT = 49.05 N
Therefore, the tension force acting on a wooden plank is 49.05 N.
Problem #2
A 6 kg book hangs from a string and undergoes an acceleration of 4 m/s2 in the downward direction. Determine the tension force acting on the book.
Solution
Given data:
- Mass of the book, m = 6 kg
- Acceleration of the book, a = 4 m/s2
- Tension force acting on the book, FT = ?
Using the equation, when an object is moving downward:
- FT = mg – ma
- FT = (6 × 9.81) – (6 × 4)
- FT = 58.86 – 24
- FT = 34.86 N
Therefore, the tension force acting on the book is 34.86 N.
Problem #3
A 3 kg metal sphere hangs from a rope, accelerating upward at a rate of 15 m/s2. Calculate the tension force acting on the sphere, considering the gravitational acceleration, g, to be 9.81 m/s2.
Solution
Given data:
- Mass of the metal sphere, m = 3 kg
- Acceleration of the metal sphere, a = 15 m/s2
- Tension force acting on the metal sphere, FT = ?
- Gravitational acceleration, g = 9.81 m/s2
Using the equation, when an object is moving upward:
- FT = mg + ma
- FT = (3 × 9.81) + (3 × 15)
- FT = 29.43 + 45
- FT = 74.43 N
Therefore, the tension force acting on the metal sphere is 74.43 N.
Problem #4
Calculate the tension force acting on a 7 kg crate in the following scenarios:
(a) The crate is moving upward with an acceleration of 6 m/s2.
(b) The crate is moving downward with an acceleration of 9 m/s2.
(c) The crate is at rest.
Solution
Given data:
- Mass of a crate, m = 7 kg
- Tension force acting on a crate, FT = ?
(a) When the crate is moving upward with an acceleration of 6 m/s2
- Acceleration of a crate, a = 6 m/s2
Using the equation, when an object is moving upward:
- FT = mg + ma
- FT = (7 × 9.81) + (7 × 6)
- FT = 68.67 + 42
- FT = 110.67 N
Therefore, the tension force acting on a crate is 110.67 N.
(b) When the crate is moving downward with an acceleration of 9 m/s2
- Acceleration of a crate, a = 9 m/s2
Using the equation, when an object is moving downward:
- FT = mg – ma
- FT = (7 × 9.81) – (7 × 9)
- FT = 68.67 – 63
- FT = 5.67 N
Therefore, the tension force acting on a crate is 5.67 N.
(c) When the crate is at rest
Using the equation, when an object is at rest:
- FT = mg
- FT = 7 × 9.81
- FT = 68.67 N
Therefore, the tension force acting on a crate is 68.67 N.
Related
- Balanced force
- Unbalanced force
- Friction
- Tension (physics)
- Applied force
- Normal force
- Drag (physics)
- Gravity
- Centripetal force
- Centrifugal force
- Buoyancy
- Net force
- Compression (physics)
More topics
External links
- What is tension? (article) – Khan Academy
- Tension (physics) – Wikipedia
- 4.5 Normal, Tension, and Other Examples of Forces – OpenStax
- 2.6: Normal Force and Tension – Physics LibreTexts
- 3 Ways to Calculate Tension in Physics – wikiHow
- Tension: Meaning, Examples, Forces & Physics – Vaia
- AP Physics 1 : Tension – Varsity Tutors
- Understanding tension – Physics Stack Exchange
- Tension (Physics): Definition, Formula, How to Find (w/ Diagrams & Examples) – Sciencing
- How to Find the Force of Tension – Physics Calculations
- Tension | physics – Britannica
- Tension Equation & Overview | What is Tension in Physics? – Study.com
- Tension Force Examples – Science Facts
- Types of Forces – The Physics Classroom
- 4.5 Normal, Tension, and Other Examples of Forces – UCF Pressbooks
- Tension Formula – SoftSchools.com
- PHYS101: Tension – Saylor Academy
- Tension Calculator – Omni Calculator
- What is the formula for tension?? + Example – Socratic
- Tension: Force That Results From Stretching – StickMan Physics
- Tension Force – Physics Bootcamp
- Tension – Wizeprep
- Tension (physics) – Chem Europe
- Tension Formula| Daily Life Examples – What’s Insight
Deep
Forceinphysics.com was founded by Deep Rana, who is a mechanical engineer by profession and a blogger by passion. He has a good conceptual knowledge on different educational topics and he provides the same on this website. He loves to learn something new everyday and believes that the best utilization of free time is developing a new skill.