Normal force

by

The information on this page is ✔ fact-checked.

Normal force
Normal force demonstration | Image: Force in Physics

The normal force is a contact force that a surface exerts to support the weight of an object resting on it. It acts perpendicular to the surface and prevents the object from sinking or passing through it. For instance, imagine a boy sitting on the floor, reading a book. The normal force exerted by the floor on the boy is equal in magnitude and opposite in direction to the force the boy applies downward due to his weight. This balance ensures that the boy does not pass through the floor, as the normal force acts as a barrier, counteracting the force of gravity.

Examples

Girl

Normal force example - girl
The normal force exerted by the ground supports the girl’s weight, keeping her from sinking through the surface | Image: Force in Physics

When an individual stands on a flat surface, the surface exerts a normal force on them and provides the necessary support to prevent them from sinking through. The normal force, acting perpendicular to the surface, counteracts gravity, and keeps the person stable. This real-life example demonstrates how the normal force is at play in our daily lives, ensuring our feet remain firmly planted on the ground and maintaining equilibrium while standing.

Book

Normal force example - book
The normal force exerted by the table counteracts the force of gravity, preventing the book from falling through the table | Image: Force in Physics

When a book is placed on a flat surface like a desk or table, it experiences a normal force that prevents it from sinking through the surface. This normal force, exerted by the desk or table on the book, acts in an upward direction and is perpendicular to the surface. It counteracts the force of gravity pulling the book downward and creates a balance of forces that keeps the book in a stable position on the desk or table. The normal force serves as the supporting force, ensuring that the book remains securely positioned on a flat surface and does not fall through.

Banana crate

Normal force example - banana crate
The normal force exerted by the floor holds the crate in equilibrium and prevents it from sinking into the ground | Image: Force in Physics

When a banana crate is positioned on the floor in fruit markets, it is supported and kept from sinking through the surface by the normal force. The normal force, exerted by the floor in an upward direction and perpendicular to the surface, acts as a supporting force for the banana crate. It balances the force of gravity pulling the crate downwards, ensuring that the crate remains stably positioned on the floor. The normal force acts as a barrier and prevents the banana crate from penetrating or passing through the floor surface.

Television

Normal force example - television
The normal force exerted by the table supports the weight of the television, keeping it stable on the surface | Image: Force in Physics

Imagine a television set placed on a TV stand or table. The reason the television remains in its position without sinking through the surface is thanks to the normal force exerted by the table. The table’s surface exerts an upward force on the television, known as the normal force. This normal force acts perpendicular to the table’s surface and provides the necessary support to keep the television stable. It counterbalances the force of gravity pulling the television downward, ensuring that it stays securely placed on the table.

Flower pot

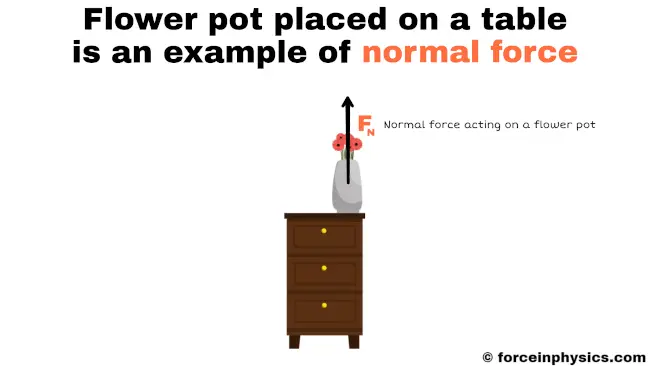
Normal force example - flower pot
The normal force exerted by the table counteracts gravity, keeping the flower pot stable on the surface | Image: Force in Physics

When a flower pot is placed on a table, the normal force comes into play. The table’s surface exerts an upward force on the flower pot, perpendicular to the table. This force, known as the normal force, supports the flower pot and prevents it from sinking into or passing through the table. The normal force ensures the pot remains securely positioned on the table’s surface; it provides stability and prevents any undesired movement.

Equation

The normal force equation is used for calculating the force exerted on an object in different situations. For an object resting on a flat surface, the equation simplifies to FN = mg, where FN represents the normal force, m is the mass of the object, and g is the acceleration due to gravity. When the object is on an inclined surface at an angle α, the equation becomes FN = mg × cos(α).

In scenarios involving external forces, the normal force equation can be modified accordingly. If a downward external force is applied to an object, the equation becomes FN = mg + F sin(θ), with F denoting the magnitude of the external force and θ representing the angle between the horizontal surface and the direction of the external force. Conversely, if an upward external force acts on the object, the equation becomes FN = mg – F sin(θ). The measurement unit for the external force, F, is newton (N), while α and θ are measured in degrees. By using these normal force equations, one can accurately calculate the normal force exerted on an object in various scenarios.

Practice problems

Problem #1

Determine the normal force acting on a 5 kg box positioned on an inclined surface inclined at an angle of 30°.

Solution

Given data:

  • Normal force acting on the box, FN = ?
  • Mass of the box, m = 5 kg
  • Angle of an inclined surface, α = 30°

Applying the equation, when an object is placed on an inclined surface:

  • FN = mg × cos (α)
  • FN = 5 × 9.81 × cos (30°)
  • FN = 49.05 × 0.1542
  • FN = 7.56 N

Therefore, the normal force acting on the box is 7.56 N.

Problem #2

Find the normal force exerted on a 4 kg toolbox resting on a workbench. The gravitational acceleration is given as g = 9.81 m/s2.

Solution

Given data:

  • Normal force acting on the toolbox, FN = ?
  • Mass of the toolbox, m = 4 kg
  • Gravitational acceleration, g = 9.81 m/s2

Applying the equation, when an object is resting on the flat surface:

  • FN = mg
  • FN = 4 × 9.81
  • FN = 39.24 N

Therefore, the normal force acting on the toolbox is 39.24 N.

Problem #3

Calculate the normal force acting on a 6 kg book when an external upward force of 15 N is applied at a 60° angle.

Solution

Given data:

  • Normal force acting on the book, FN = ?
  • Mass of the book, m = 6 kg
  • External upward force applied on the book, F = 15 N
  • Angle between horizontal surface and external upward force, θ = 60°

Applying the equation, when an external upward force is acting on an object:

  • FN = mg – F sin (θ)
  • FN = [6 × 9.81] – [15 × sin (60°)]
  • FN = 58.86 – [15 × (-0.3048)]
  • FN = 58.86 – (-4.572)
  • FN = 58.86 + 4.572
  • FN = 63.43 N

Therefore, the normal force acting on the book is 63.43 N.

Problem #4

An external downward force of 12 N is applied at a 20° angle to a metal crate with a mass of 25 kg, resting on the ground. Determine the normal force acting on the metal crate.

Solution

Given data:

  • External downward force applied on the metal crate, F = 12 N
  • Angle between horizontal surface and external downward force, θ = 20°
  • Mass of the metal crate, m = 25 kg
  • Normal force acting on the metal crate, FN = ?

Applying the equation, when an external downward force is acting on an object:

  • FN = mg + F sin (θ)
  • FN = [25 × 9.81] + [12 × sin (20°)]
  • FN = 245.25 + [12 × 0.9129]
  • FN = 245.25 + 10.9548
  • FN = 256.20 N

Therefore, the normal force acting on the metal crate is 256.20 N.

Related

More topics

External links

Deep

Forceinphysics.com was founded by Deep Rana, who is a mechanical engineer by profession and a blogger by passion. He has a good conceptual knowledge on different educational topics and he provides the same on this website. He loves to learn something new everyday and believes that the best utilization of free time is developing a new skill.

Leave a Comment