Drag (physics)

by

The information on this page is ✔ fact-checked.

Drag (physics)
Drag force demonstration | Image: Force in Physics

In physics, drag, also known as fluid resistance, is a physical force that opposes the motion of an object as it moves through a fluid, such as air or water. When the object travels through the fluid, the fluid molecules interact with its surface and create a force of resistance that acts in the opposite direction to its movement. The magnitude of drag depends on factors like the object’s speed, size, and shape. For instance, consider a paper plane flying through the air. As the paper plane moves forward, the air molecules exert a drag on its surface, making it harder for the paper plane to maintain its velocity and stay airborne. Drag significantly affects the flight characteristics of the paper plane. It slows down and alters its trajectory. Drag is a fundamental factor in various phenomena, such as the flight of airplanes, the motion of vehicles, and the behavior of aquatic creatures in water.

Examples

Flower petals

Drag example - flower petals
Drag slows down the petals’ descent, causing them to flutter in the air | Image: Force in Physics

When flower petals are gently tossed into the air, gravity begins to pull them downwards, as expected. However, as they descend, the surrounding air pushes against the motion, creating a resistance force known as air drag. This air drag counters the effect of gravity and slows down the petals’ descent. As a result, the flower petals appear to float gracefully in the air for a brief moment before they eventually reach the ground. The interplay between gravity and air drag influences the petals’ trajectory and showcases how drag impacts the motion of objects through the air.

Floating paper

Drag example - floating paper
Drag acts against the paper’s motion, making it fall more slowly | Image: Force in Physics

When small pieces of paper are thrown into the air, they experience the force of gravity pulling them downward. However, as they travel through the air, they also encounter resistance from the air itself. This resistance, known as air drag, opposes their motion and slows down their descent. The interplay between gravity and air drag creates an interesting dynamic, where the paper pieces appear to float and flutter in the air, defying a swift fall. The magnitude of air drag depends on factors such as the size, shape, and weight of the paper pieces, as well as the air density and speed of their motion. Consequently, these small paper pieces exhibit a graceful, almost dance-like descent as they respond to the forces of gravity and air drag.

Airplane

Drag example - airplane
Drag opposes the airplane’s forward motion, requiring more thrust from the engines | Image: Force in Physics

Airplanes experience air resistance, also known as drag, during flight. As they move forward, the surrounding air exerts a force in the opposite direction and slows them down. This resistance is caused by the interaction between the airplane’s structure and the air. The magnitude of drag is determined by various factors, such as the airplane’s shape, size, speed, and the density of the air.

The consideration of drag is essential in aviation to optimize fuel efficiency and overall performance. Engineers and pilots take drag into account when designing airplanes and planning flight routes. Aviation professionals can ensure smoother and more efficient flights by understanding and managing drag. Minimizing drag and maximizing aerodynamic performance allow airplanes to travel more efficiently. This saves fuel and enhances the overall flight experience.

Moving car

Drag example - moving car
Drag resists the hand’s motion, making it difficult to move through the air | Image: Force in Physics

When a hand is extended out of a moving car, it experiences drag. As the car moves forward, the hand encounters the air in front of it, and the air pushes against the hand in the opposite direction. This interaction between the hand and the surrounding air creates a backward force known as drag. The faster the car moves, the stronger the drag force becomes, making it more challenging to keep the hand extended steadily.

Falling leaf

Drag example - falling leaf
Drag slows down the leaf’s descent, causing it to sway as it falls | Image: Force in Physics

When a leaf falls from a tree, it encounters the force of air resistance, commonly known as drag. As the leaf descends, the air surrounding it generates an upward force, which counters the force of gravity pulling it downward. This opposing force allows the leaf to float and linger in the air for a brief period before it eventually completes its descent and lands on the ground. The interaction between gravity and air resistance influences the leaf’s motion; it creates a gentle and slow descent and showcases the impact of drag on objects moving through the air.

Walking

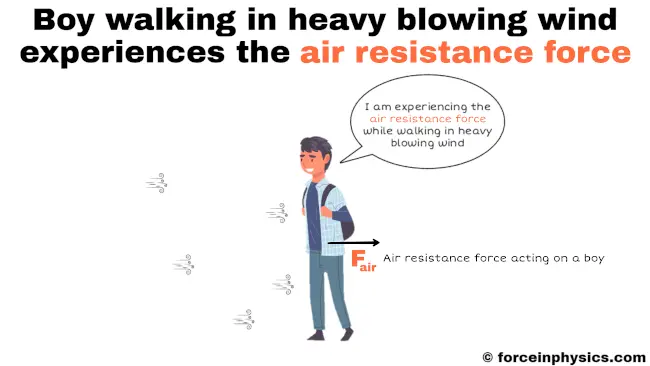
Drag example - walking
Drag opposes the person’s forward motion, making walking more challenging | Image: Force in Physics

When people walk against strong winds, they encounter the effect of air resistance. As they move forward, the air surrounding them generates a resistance force, pushing back against their motion. This resistance force, commonly referred to as air resistance or drag, hinders their progress and makes it more challenging to walk against the wind. The force of the wind acting in the opposite direction creates a sensation of being pushed backward, highlighting the impact of drag on human movement in windy conditions.

Bicycle ride

Drag example - bicycle ride
Drag hinders the bicycle’s progress, requiring more effort from the cyclist | Image: Force in Physics

When a cyclist rides their bicycle into a headwind, they experience the force of air resistance. As the bicycle moves forward, the air in the opposite direction, exerting this force, hinders the cyclist’s progress and reduces their speed. Air resistance acts as a resistance force that opposes the motion of the bicycle and the rider. Cyclists may need to exert extra effort and pedal harder to overcome this resistance and maintain their forward motion efficiently, especially in windy conditions.

Paragliding

Drag example - paragliding
Drag acts against the paraglider’s descent, controlling the speed of the descent | Image: Force in Physics

During paragliding, when a parachutist jumps from a height and deploys the parachute, they encounter the force of drag. As they descend, the surrounding air exerts an upward force known as drag, acting against the force of gravity. This drag force effectively slows down the parachutist’s descent and allows for a controlled and smooth glide through the air until a gentle landing is achieved. The parachute’s design and larger surface area play a significant role in increasing the drag force experienced, which results in a safer and more enjoyable paragliding experience.

Equation

The drag equation, also referred to as the drag force formula or air resistance formula, is a mathematical expression given as FD = ½ × ρ A CD v2. In this equation, FD stands for the drag force experienced by an object as it moves through a fluid, like air. The variables ρ, A, CD, and v represent the fluid density, the object’s cross-sectional area, the drag coefficient, and the object’s velocity, respectively. By utilizing this equation, it becomes possible to calculate the drag force, which signifies the resistance encountered by an object while it traverses through the fluid.

Practice problems

Problem #1

Find the drag force experienced by a falling paper plane traveling at a velocity of 7 m/s. The air’s density is 1.10 kg/m3, the paper plane’s cross-sectional area is 0.015 m2, and the drag coefficient is 0.03.

Solution

Given data:

  • Drag force acting on the paper plane, FD = ?
  • Velocity of the paper plane, v = 7 m/s
  • Density of the air, ρ = 1.10 kg/m3
  • Cross sectional area of the paper plane, A = 0.015 m2
  • Drag coefficient, CD = 0.03

Using the equation:

  • FD = ½ × ρ A CD v2
  • FD = ½ × 1.10 × 0.015 × 0.03 × (7)2
  • FD = 0.01 N

Therefore, the drag force acting on the paper plane is 0.01 N.

Problem #2

Determine the drag force on a descending sky lantern moving at a velocity of 1 m/s. Take into account the air’s density of 1.28 kg/m3, the sky lantern’s cross-sectional area of 0.18 m2, and the drag coefficient of 0.65.

Solution

Given data:

  • Drag force acting on the sky lantern, FD = ?
  • Velocity of the sky lantern, v = 1 m/s
  • Density of the air, ρ = 1.28 kg/m3
  • Cross sectional area of the sky lantern, A = 0.18 m2
  • Drag coefficient, CD = 0.65

Using the equation:

  • FD = ½ × ρ A CD v2
  • FD = ½ × 1.28 × 0.18 × 0.65 × (1)2
  • FD = 0.07 N

Therefore, the drag force acting on the sky lantern is 0.07 N.

Problem #3

Calculate the drag force experienced by a feather-like plastic bag descending with a velocity of 2 m/s. Consider the air density as 1.20 kg/m3, the bag’s cross-sectional area as 0.10 m2, and the drag coefficient as 0.06.

Solution

Given data:

  • Drag force acting on the plastic bag, FD = ?
  • Velocity of the plastic bag, v = 2 m/s
  • Density of the air, ρ = 1.20 kg/m3
  • Cross sectional area of the plastic bag, A = 0.10 m2
  • Drag coefficient, CD = 0.06

Using the equation:

  • FD = ½ × ρ A CD v2
  • FD = ½ × 1.20 × 0.10 × 0.06 × (2)2
  • FD = 0.01 N

Therefore, the drag force acting on the plastic bag is 0.01 N.

Problem #4

Find the drag force acting on a kite as it falls with a velocity of 1.5 m/s after being released from a hilltop. Take into account the air density as 1.19 kg/m3, the kite’s cross-sectional area as 0.25 m2, and the drag coefficient as 0.10.

Solution

Given data:

  • Drag force acting on the kite, FD = ?
  • Velocity of the kite, v = 1.5 m/s
  • Density of the air, ρ = 1.19 kg/m3
  • Cross sectional area of the kite, A = 0.25 m2
  • Drag coefficient, CD = 0.10

Using the equation:

  • FD = ½ × ρ A CD v2
  • FD = ½ × 1.19 × 0.25 × 0.10 × (1.5)2
  • FD = 0.03 N

Therefore, the drag force acting on the kite is 0.03 N.

Related

More topics

External links

Deep

Forceinphysics.com was founded by Deep Rana, who is a mechanical engineer by profession and a blogger by passion. He has a good conceptual knowledge on different educational topics and he provides the same on this website. He loves to learn something new everyday and believes that the best utilization of free time is developing a new skill.

Leave a Comment